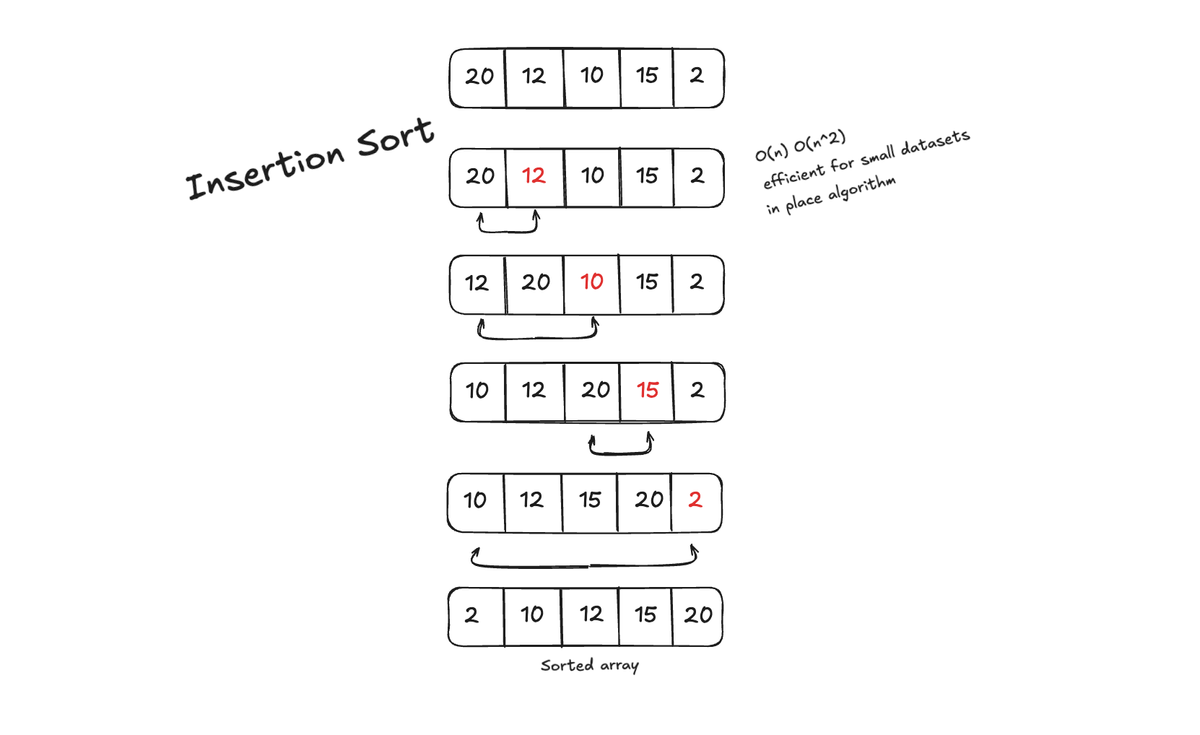
Algorithms: Heap sort

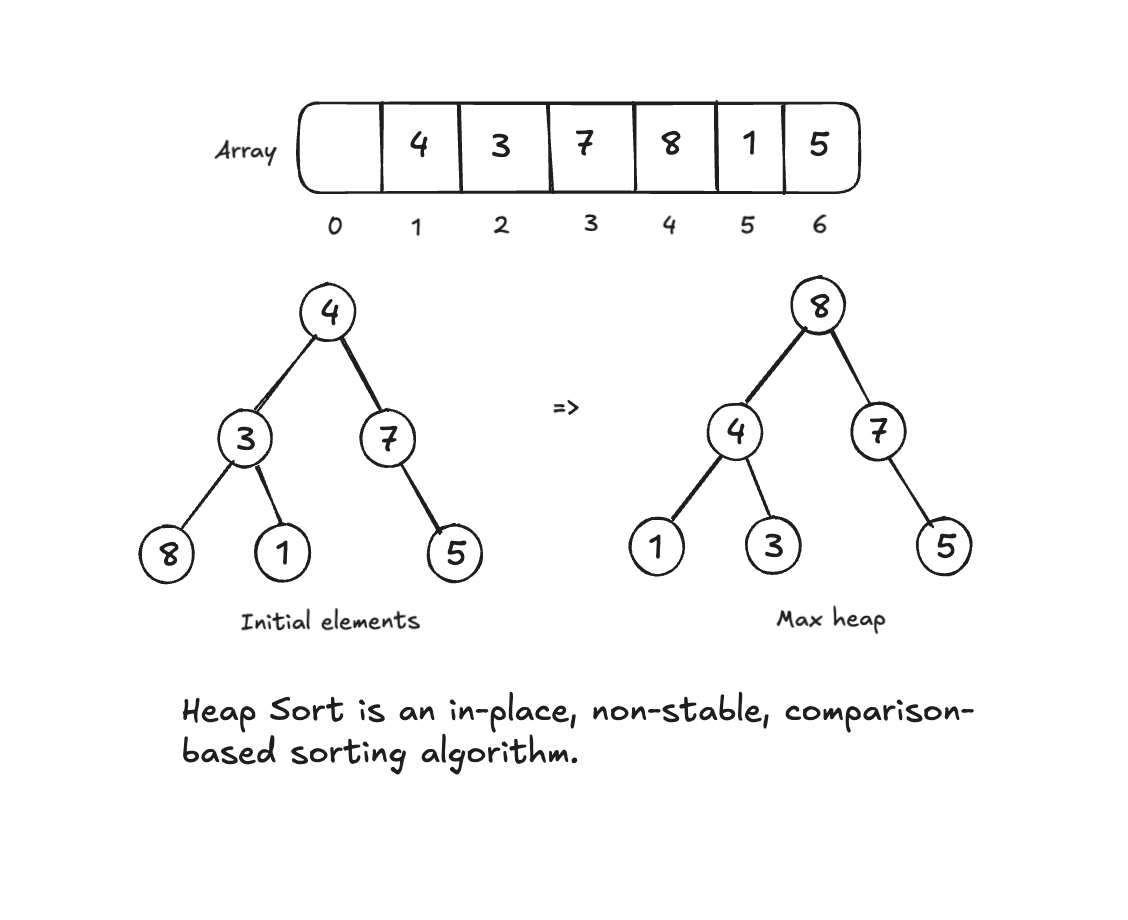
The Heap sort algorithm is based on the idea of repeatedly extracting the largest or the smallest element from a heap and then reconstructing the heap.

But what is a heap? A heap is specialised binary tree-based data structure. heap property dictates the relationship between a parent node and its children.

We can split the heap into two. A Max-heap and a Min-heap.

Max-Heap: Every parent node is greater than or equal to its children. This means the largest element is at the root of the heap.
Min-Heap: Every parent node is less than or equal to its children. This means the smallest element is at the root of the heap.

A Heap is always a Complete Binary Tree. This means all levels of the tree are fully filled with possible exception of the last level, which is filled from left to right.

So why is a Complete Binary Tree required here?

For a Max-Heap and Min-Heap we need a structure where every parent node satisfies the heap property and relation and respect to its children.
With a Complete Binary Tree we ensure minimal height for efficient comparison and swapping.

Example Nodes: [1, 2, 3, 4, 5, 6].

Complete Binary Tree

Non Complete Binary Tree

Lets look at some code here for Heap sort.

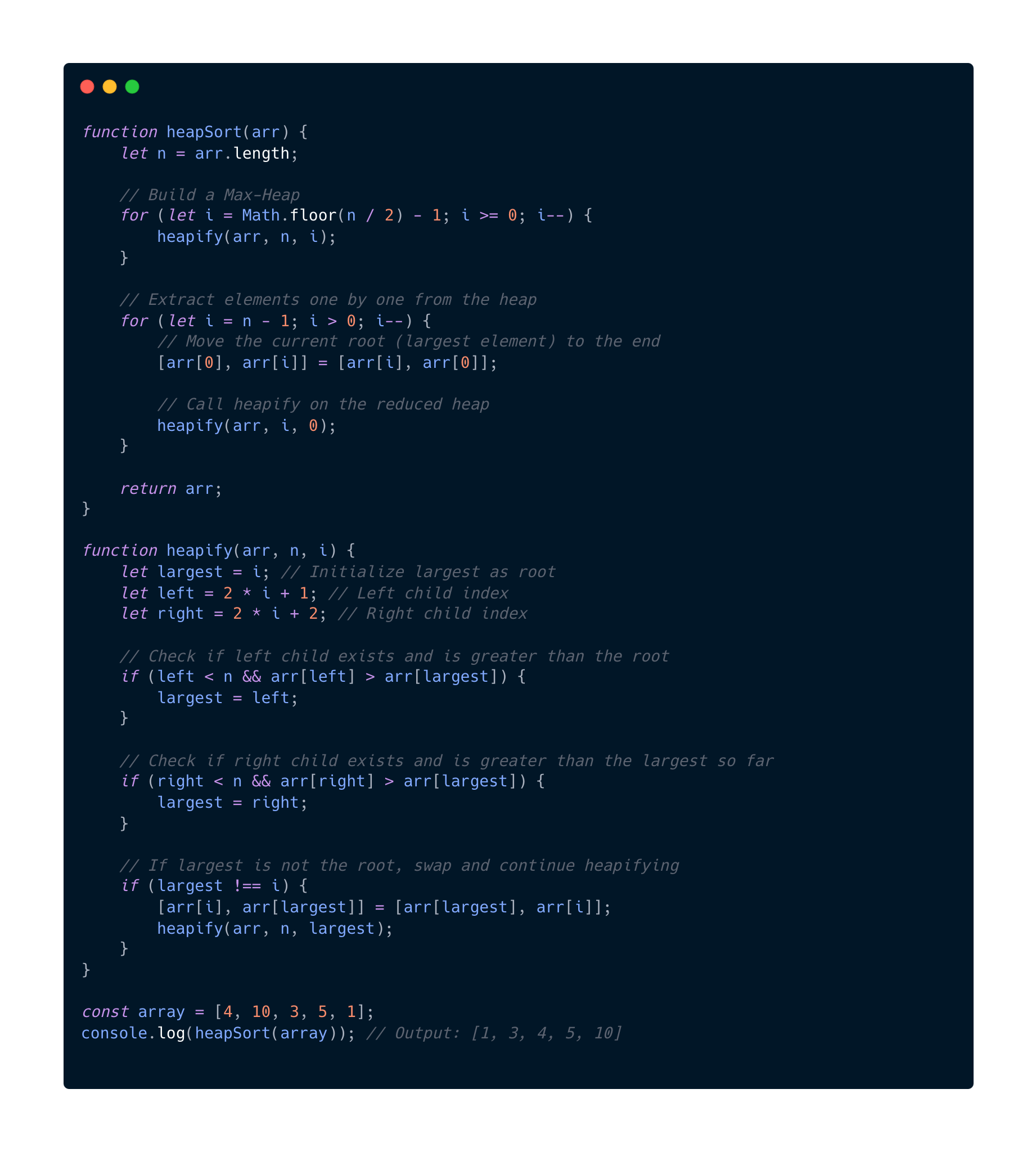
So now when we understand the basics of Heap sort and the complexity that comes with it we must practice this together.

Here is some basic -> Expert exercises for Heap Sort

Heap Sort Complexity

Algorithm	Time Complexity (Best)	Time Complexity (Worst)	Space Complexity	Stable?
Heap Sort	O(n log n)	O(n log n)	O(1) (in-place)	No

Comparison with other sorting algorithms

Algorithm	Time Complexity (Best)	Time Complexity (Worst)	Space Complexity	Stable?
Selection	$O(n^2)$	$O(n^2)$	$O(1)$	No
Bubble	$O(n)$ (optimized)	$O(n^2)$	$O(1)$	Yes
Insertion	$O(n)$	$O(n^2)$	$O(1)$	Yes
Merge	$O(n \log n)$	$O(n \log n)$	$O(n)$	Yes
Quick	$O(n \log n)$	$O(n^2)$	$O(\log n)$	No

So now when we understand the basics of Heap sort and the complexity that comes with it we must practice this together.

Here is some basic -> Expert exercises for Heap Sort

Github Heap Sort

Sign up for Andreas Jangefalk