Algorithms: Merge Sort

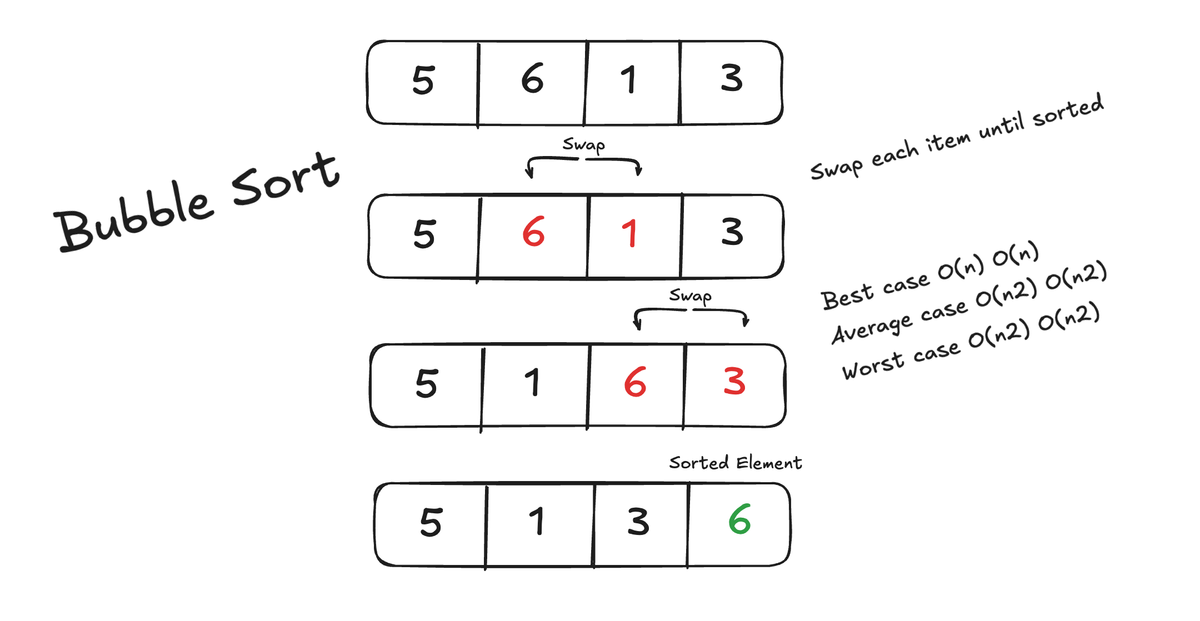
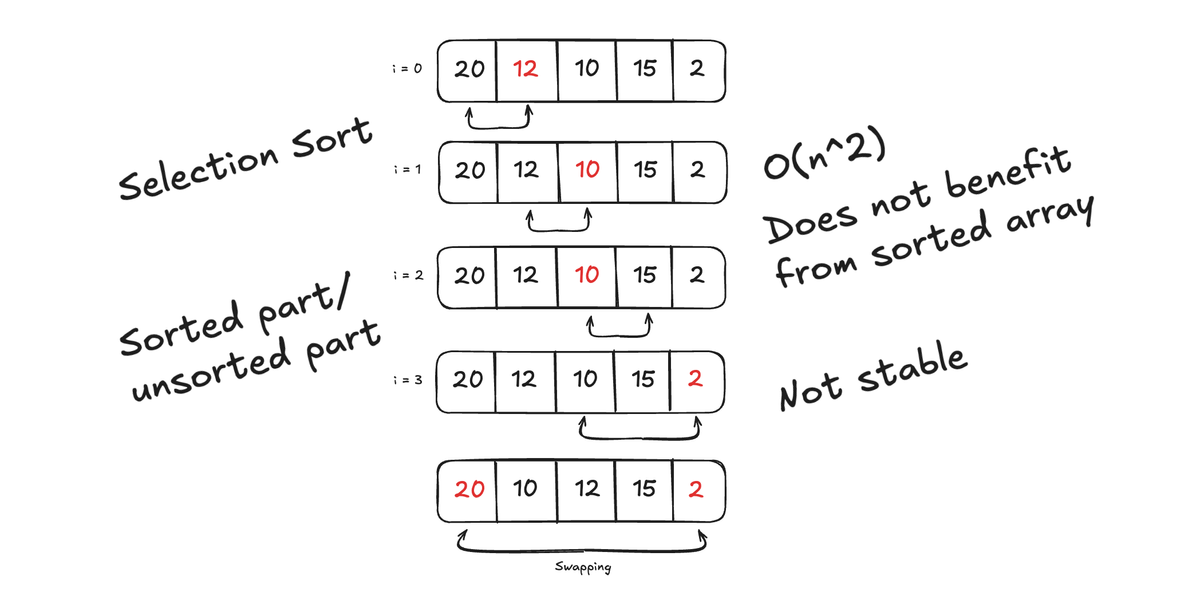
Now we have goon through Bubble sort and Selection sort and as we have learned it is not efficient algorithms by any means. Selection sort is even unstable. So lets turn our perspective to one of the most efficient sorting algorithms. Let me introduce the Merge sort algorithm.

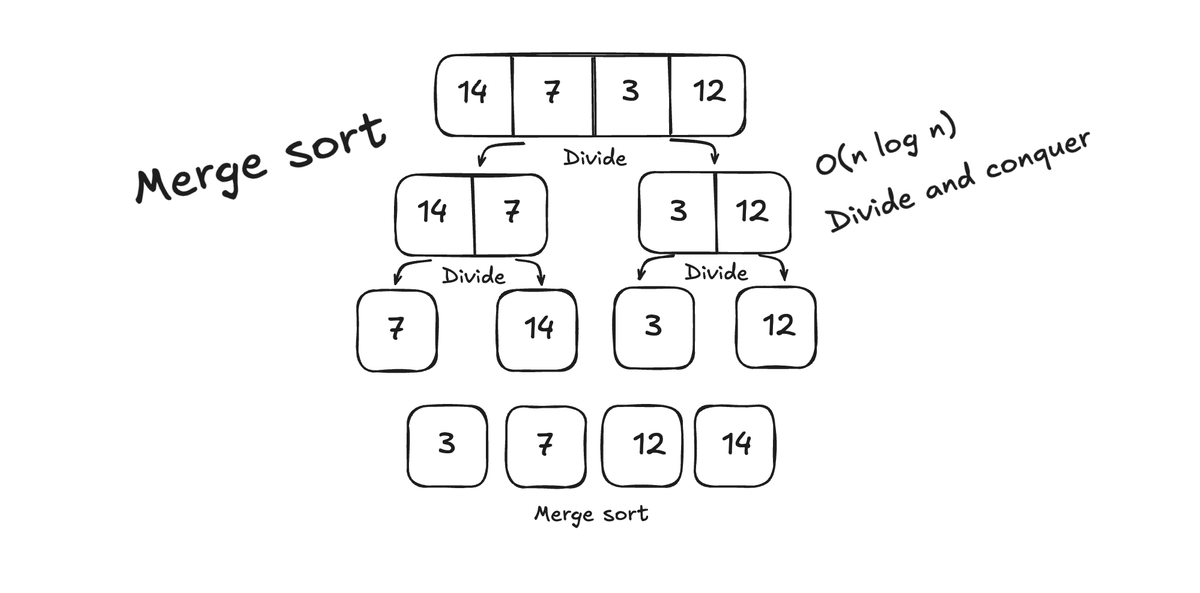
Merge sort is a divide-and-conquer algorithm. It works by dividing the input array into smaller subarrays, then sort each subarray and then merges the sorted subarray to produce the final result.

The algorithm has three steps of actions.

Divide - Here we are splitting into two halves until each subarray contains a single element. This is also known as base case
Conquer - Here we recursively sort each subarray.
Combine - The final step consists of merging the sorted subarrays back together to a final sorted array.

When talking about time complexity for best case, average case and worst case we can see the following.

Best case O(n log n)
Average case O(n log n)
Worst case O(n log n)

Since merge sort requires additional memory for temporary arrays during the merge we will end up with O(n) for space complexity.

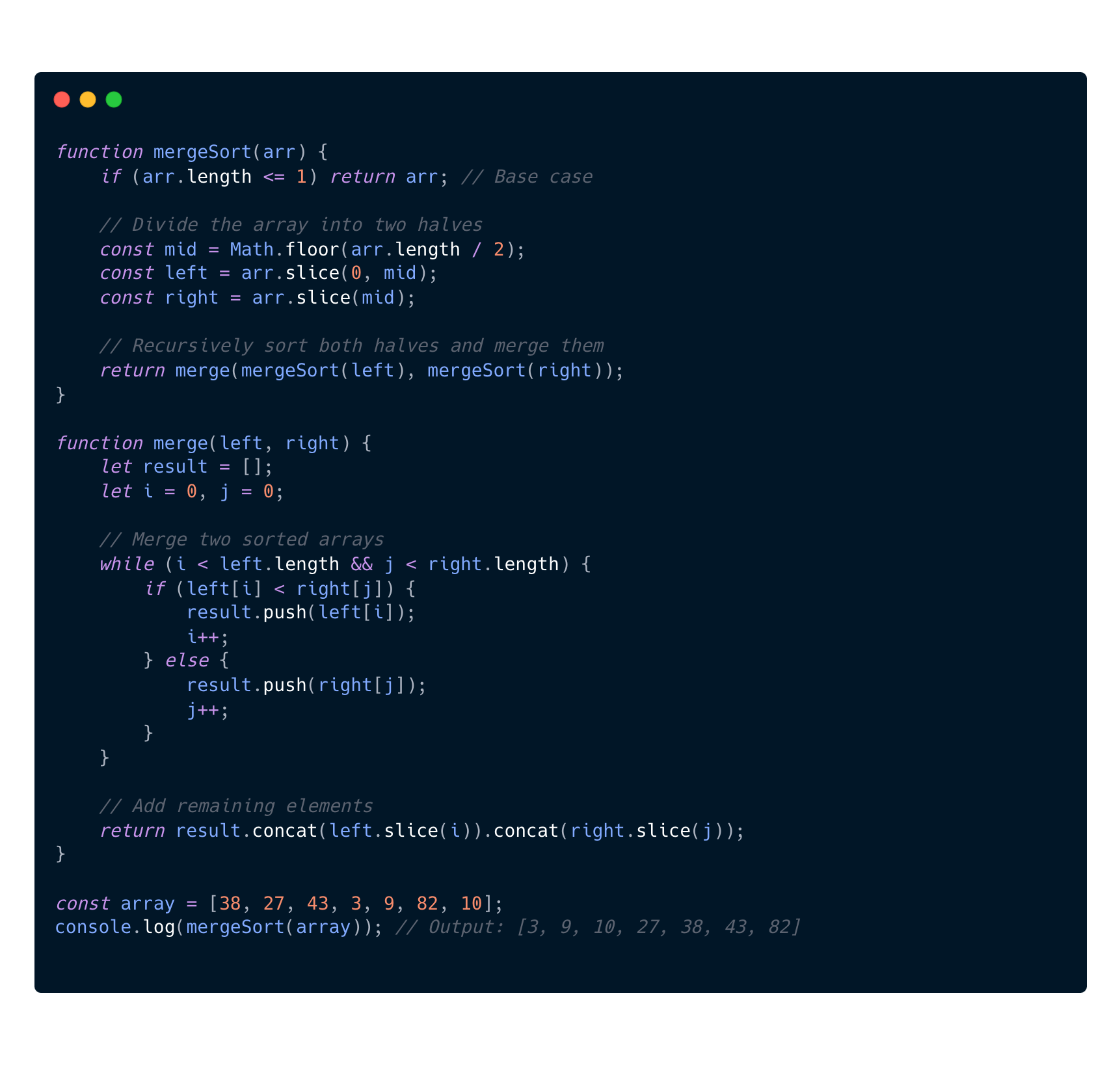
If we look at this code we can see that we are running the diving and merging recursively to be able to get a final sorted array.

The merge sort algorithm thieves in the following areas:

Predictable performance O(n log n)
Good for large datasets
Stable
Good for parallelisation.

But with great pros a few cons arrive

Space-complexity because of additional memory is needed.
Not In-Place

Comparison with Other Sorting Algorithms

Algorithm	Time Complexity (Best)	Time Complexity (Worst)	Space Complexity	Stable?
Selection	$O(n^2)$	$O(n^2)$	$O(1)$	No
Bubble	$O(n)$ (optimized)	$O(n^2)$	$O(1)$	Yes
Insertion	$O(n)$	$O(n^2)$	$O(1)$	Yes
Merge	$O(n \log n)$	$O(n \log n)$	$O(n)$	Yes
Quick	$O(n \log n)$	$O(n^2)$	$O(\log n)$	No

So now when we understand the basics of Merge sort and the complexity that comes with it we must practice this together.

Here is some basic -> Expert exercises for Merge Sort

Github Merge Sort

Comparison with Other Sorting Algorithms

Sign up for Andreas Jangefalk