Algorithms: Selection Sort

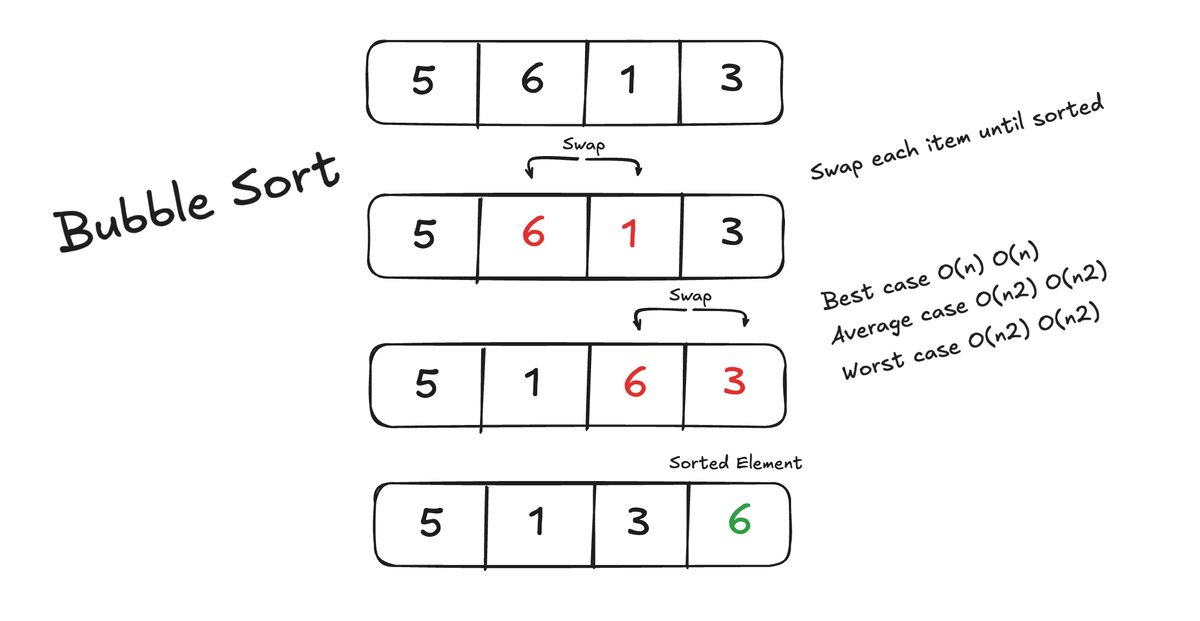
Now when we have visited the Bubble sort algorithm is time for the next one in line and it is pretty similar but have its differences.

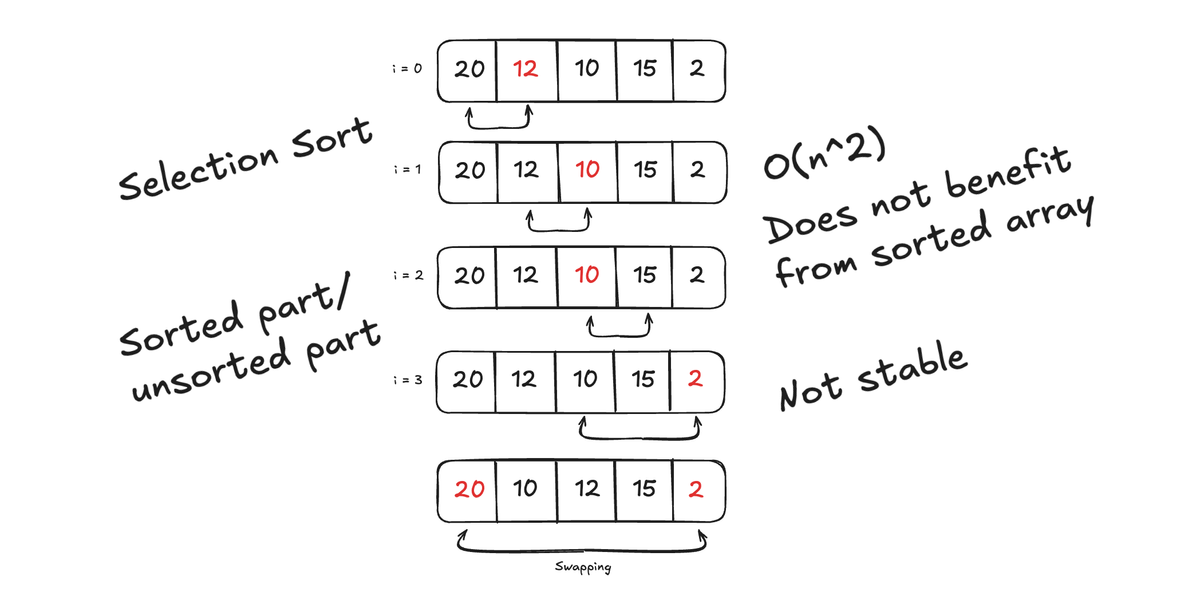
A selection sort algorithm is a simple comparison-based sorting algorithm. It works by dividing a list into two parts.

The sorted part (from left to right)
The unsorted part

When iterating each step the algorithm finds the smallest or largest element (depending on the order) in the unsorted part and then swaps it with the first element of the unsorted part. When doing this for each iteration the sorted part will grow and unsorted part will reduce.

When iterating through a list [30, 25, 1, 5, 45, 17, 19] the step by step process would look like

Find the smallest element (1) and swap it with the first element in the list (30) result [1, 25, 30, 5, 45, 17, 19]
Find the next smallest number (5) and swap it with the second element (25) etc.

When talking about complexity in the Selection sort algorithm we can see the following result.

Case	Comparisons	Swaps	Time Complexity
Best Case	$O(n^2)$	$O(n)$	$O(n^2)$
Average Case	$O(n^2)$	$O(n)$	$O(n^2)$
Worst Case	$O(n^2)$	$O(n)$	$O(n^2)$

For the one who is following a question could arise why it is O(n^2)?

It is because, for each of the elements this algorithm need to search through the unsorted part of the list to find the smallest element. That will result in a quadratic Growth in comparisons as n increases.

Lets look at some code :

Key takeaways for Selection sort:

Selection sort is a In-place algorithm and doesn't require extra space for another array. It will just act on the list itself.
Not stable. It can result in faulty behaviours when dealing with equal elements.
Used for small datasets when simplicity is important
If stability is not an issue.
When memory is limited.
Does not benefit from a sorted or nearly sorted array.

Comparison with other sorting algorithms

Algorithm	Time Complexity (Best)	Time Complexity (Worst)	Space Complexity	Stable?
Selection	$O(n^2)$	$O(n^2)$	$O(1)$	No
Bubble	$O(n)$ (optimized)	$O(n^2)$	$O(1)$	Yes
Insertion	$O(n)$	$O(n^2)$	$O(1)$	Yes
Merge	$O(n \log n)$	$O(n \log n)$	$O(n)$	Yes
Quick	$O(n \log n)$	$O(n^2)$	$O(\log n)$	No

So now when we understand the basics of Selection sort and the complexity that comes with it we must practice this together.

Here is some basic -> Expert exercises for Selection Sort

Github Selection Sort

Sign up for Andreas Jangefalk